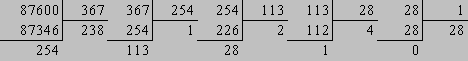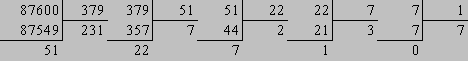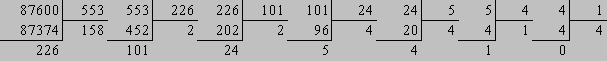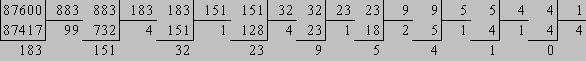| Заказать
курсач за 10 грн. ДИСК 1-6 семестр 250 грн ДОБАВЬ СВОЕ ФОТО регистрация KIS-Plus вход в KIS PLUS новости |
Університет інформаційно - комунікаційних технологій курсовой по связи, модуль , комплексное по связи, контрольная по связи, дипломный проэкт по телекомуникации, Курсовой проэкт, телекоммуникация и связь, Киевский Институт Связи, Государственный университет информационно-коммуникационных технологий, ГУИКТ, ДУІКТ, Связь, Zosik, KIS-kiev.narod.ru |
страница: 1, 2,
3, 4, 5
алгоритм шифрования
задача 1 MathCad (*.mcd)
задача 2 MathCad (*.mcd)
задача 3MathCad (*.mcd)
Задача 2
Кодирование и декодирование в асимметричной криптосистеме RSA.
1 . Выбор простых чисел P и Q .
Число L определяется как объединение множеств символов двух чисел :
L = { NГР , NСТ } [ 1.1 ]
где : NГР = 4 ( 10 ) = 100 ( 2 ) - номер группы, три разряда ;
NСТ = 21 ( 10 ) = 10101 ( 2 ) - номер студента по списку, пять разрядов.
L (2) = 10010101
L(10) = 149
Формируем числа P’ и Q’ :
P’ = ( L + 256 )2 mod 103 [ 1.2 ]
P’ = ( 149 + 256 )2 mod 103 = 25
Q’ = ( 5 ´ L + 129 )2 mod 103 [ 1.3 ]
Q’ = ( 5 ´ 149 + 129 )2 mod 103 = 876
Выбираем ближайшее большее трёхзначное простое число ( исходя из условий, что P > P’ и Q > Q’) :
P = 101
Q = 877
Вычисляем число N :
N = P ´ Q [ 1.4 ]
N = 101´ 877 = 88 577
2 . Выбор пяти пар ключей ( КО и КЗ ).
В асимметричной криптосистеме используется концепция однонаправленных функций - отсутствует алгоритм обратного преобразования с помощью кодирую -щего ключа ( или системы ключей ). Получателю передаются закодированная информация и открытый ключ К0 .
Выбор открытого ключа осуществляется выходя из условия :
1 < К0 < j (N ) [ 2.1 ]
НОД [К0 , j (N )] = 1
где : j (N ) = (P -1 ) ´ (Q - 1 ) [ 2.2 ]
j (N ) = (101 -1 ) ´ (877 - 1 ) = 87600
НОД - наибольший общий делитель
Для выбора открытого ключа К0 , взаимно прочтого числу j (N ), используем алгоритм Эвклида нахождения НОД ( методом деления ):
КО-1 = 367
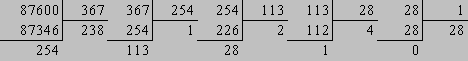
КО-2 = 379
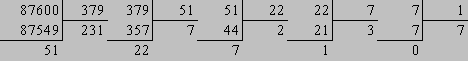
КО-3 = 431
КО-4 = 553
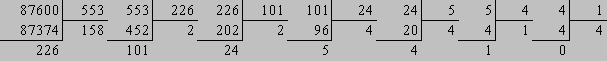
КО-5 = 883
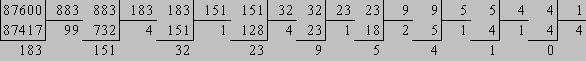
После выбора открытого ключа К0 рассчитывается ( как пара к К0 ) закрытый ключ КЗ , исходя из условия , что :
(КЗ ´ К0) mod j (N ) = 1
отсюда :
КЗ = ( 1 / К0) mod j (N ) [ 2.3 ]
Модуль числа типа ( 1 / а = а-1 ) определяется с помощью расширенного ал -горитма Эвклида для взаимно простых чисел ( Рис 4 ),
где : r = (а-1) mod b T = ( t1 , t3 )
U = ( u1 , u3 ) V = ( v1 , v3 )
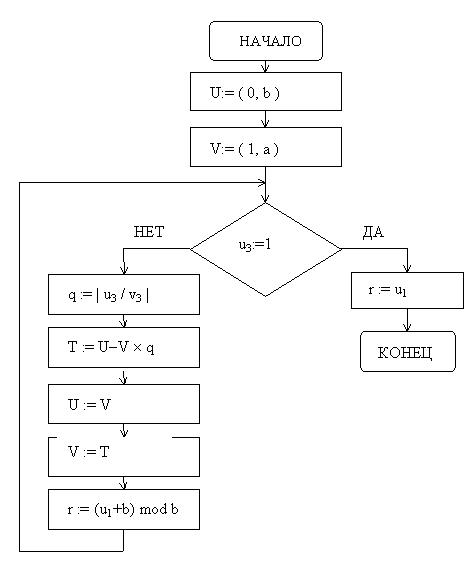
Рис 4.
По формуле [ 2.3] и используя расширенный алгоритм Эвклида ( Рис 4 ) , для простых чисел P , Q и выбранных ключей К0 расчитываем пять закрытых ключей КЗ :
страница: 1, 2,
3, 4, 5
алгоритм шифрования
задача 1 MathCad (*.mcd)
задача 2 MathCad (*.mcd)
задача 3MathCad (*.mcd)
|
|
||||
|
||||
|
|
||||
|
|
||||
|
