4.1. Сигнал з виходу АЦП надходить на вхід кодера завадостійкого коду. В дискретному каналі зв'язку використовується завадостійке кодування систематичним кодом (10.6) або (11.7) з мінімальною кодовою відстанню

d₀=3. Для трьох рівнів квантування, заданих у таблиці, записати кодові комбінації на виході завадостійкого кодера. Виробляючі матриці кодів:

Визначити відстані між комбінаціями на вході кодера та між комбінаціями на його виході. Визначте тривалість символу на виході кодера завадостійкого коду.

4.2. Розрахуйте імовірності однократних та двократних помилок на вході декодера. Зробіть висновок про те, чи поліпшиться завадостійкість прийому при виправленні декодером однократних помилок.

Решение:

Кодируемые уровни

22 0 0 1 0 1 1 0

30 0 0 1 1 1 1 0

82 1 0 1 0 0 1 0

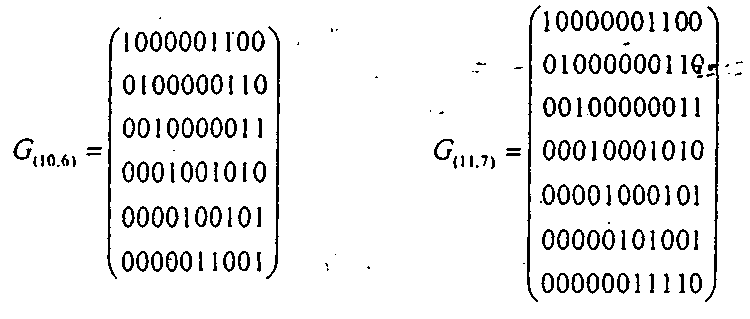
Производящая матрица : Проверочная матрица:

Находим поверочные разряды:

r_22,1=01Å 00Å 10Å 01Å 11Å 10Å 01= 1

r_22,2=01Å 01Å 10Å 00Å 11Å 10Å 01= 1

r_22,3=00Å 01Å 11Å 01Å 10Å 10Å 01= 1

r_22,4=00Å 00Å 11Å 00Å 11Å 11Å 00= 1

r_30,1=01Å 00Å 10Å 11Å 11Å 10Å 01= 0

r_30,2=01Å 01Å 10Å 10Å 11Å 10Å 01= 1

r_30,3=00Å 01Å 11Å 11Å 10Å 10Å 01= 0

r_30,4=00Å 00Å 11Å 10Å 11Å 11Å 00= 1

r_82,1=11Å 00Å 10Å 01Å 01Å 10Å 01= 1

r_82,2=11Å 01Å 10Å 00Å 01Å 10Å 01= 1

r_82,3=10Å 01Å 11Å 01Å 00Å 10Å 01= 1

r_82,4=10Å 00Å 11Å 00Å 01Å 11Å 00= 0

На выходе кодера получим кодовые комбинации:

22 0 0 1 0 1 1 0 1 1 1 1

30 0 0 1 1 1 1 0 0 1 0 1

82 1 0 1 0 0 1 0 1 1 1 0

Определим кодовое расстояние между комбинациями на входе кодера:

22 0 0 1 0 1 1 0

0 0 0 1 0 0 0

d=1

30 0 0 1 1 1 1 0

1 0 0 1 1 0 0

d=3

82 1 0 1 0 0 1 0

1 0 0 0 1 0 0

d=2

Определим кодовое расстояние между комбинациями на выходе кодера:

22 0 0 1 0 1 1 0 1 1 1 1

0 0 0 1 0 0 0 1 0 1 0

d=3

30 0 0 1 1 1 1 0 0 1 0 1

1 0 0 1 1 0 0 1 0 1 1

d=6

82 1 0 1 0 0 1 0 1 1 1 0

1 0 0 0 1 0 0 0 0 0 1

d=3

Длительность символа на выходе кодера помехоустойчивого кода:

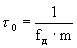
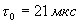
Данный помехоустойчивый код с минимальным кодовым расстоянием d₀=3 обеспечивает исправление однократных ошибок.

Рассчитаем вероятности однократных и двукратных ошибок на входе декодера.

Вероятность ошибки на входе декодера определим по формуле:

, где n=11

Вероятность однократных ошибок:

Вероятность двукратных ошибок:

Из расчетов видно, что при исправлении однократных ошибок помехоустойчивость приема резко увеличится.

Принцип помехоустойчивого кодирования заключается в введении избыточности. При этом количество возможных кодовых комбинаций становится больше, чем сообщений. Часть комбинаций называются разрешенными (те, которые сформированы кодером), а часть - запрещенными (те, которые появились в результате ошибки). Благодаря этому становится возможным обнаружение и исправление ошибок на приеме. Суть процесса состоит в том, что в память кодирующего устройства записываются разрешенные кодовые комбинации выбранного кода и правило, по которому с каждым из М сообщений источника сопоставляется одна из таких комбинаций. Данное правило известно и на декодере. Получив от источника определенное сообщение, кодер отыскивает соответствующую ему комбинацию и посылает в канал. В свою очередь, декодер, приняв комбинацию, искаженную помехами, сравнивает ее со всеми М комбинациями списка и отыскивает ту из них, которая ближе остальных к принятой.

Обнаружение и исправление ошибок при матричном задании происходит с помощью синдрома ошибок. Синдром - это n-разрядное кодовое слово, полученное в результате умножения искаженного кодового слова на проверочную матрицу. Если синдром ошибок равен нулю, то данная кодовая комбинация безошибочна либо ошибка не может быть обнаружена. Ненулевой синдром ошибок однозначно указывает положение проверочного ошибочного разряда. Если установлен номер ошибочного разряда, то при поступлении этой кодовой комбинации на выход, значение этого разряда изменяется на противоположный (т.е. инвертирующий), значит ошибка исправляется.